
精通
英语
和
开源
,
擅长
开发
与
培训
,
胸怀四海
第一信赖
In mathematics, a matrix (plural matrices) is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. The individual items in a matrix are called its elements or entries.用数学术语讲,矩阵是个矩形数组,由数字、符号或表达式组成,按行列分布。矩阵内的单个元素叫做元素或入口。
In this article, we demonstrate a Java program to do almost all matrix operations like:本文代码能够实现矩阵操作,如下
This program works by entering one matrix, and then choosing the required operation to be applied to this matrix.输入数据,再操作。
In order to benefit from this article, you need to know some Java basics and some matrix basics, but also we will cover some of these basics in this article.有Java基础和矩阵基础。
In this program, we deal with matrix operations, which has been mentioned upward, and the mathematical background needed is:数学背景。
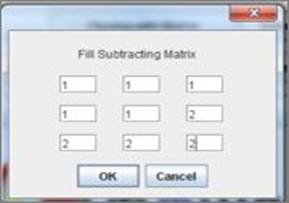
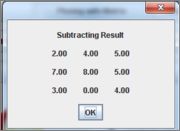
1. Matrix Addition\Subtraction加减
In matrix addition (or subtraction), the two matrices should have the same number of columns and the same number of rows.
The operation is done element by element, i.e., each element in the result is equal to the sum of the two corresponding elements in the two matrices in case of matrix addition (or their difference in case of matrix subtraction).
We see then that the result is a matrix of the same dimensions also.
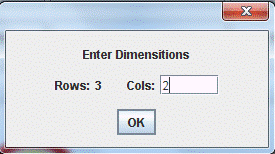
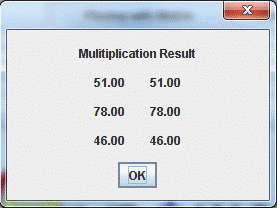
2. Matrix Multiplication乘
When multiplying a matrix by another, the number of columns in the first matrix must be equal to the number of rows in the second one. The number of rows of the result matrix is equal to the number of rows of first one while its number of columns is equal to that of the second one. You see, the multiplication is assumed to be done from one direction (from the right).
Any element of the result matrix is got by multiplying the elements of the rows of the first matrix by the corresponding elements of the corresponding columns of the second matrix, and summing these products up. This is called the "inner product" of two vectors (the row and the corresponding column multiplied by each other).
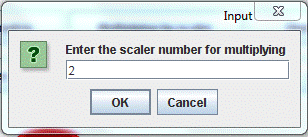
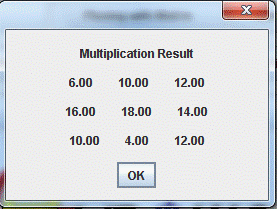
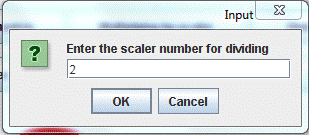
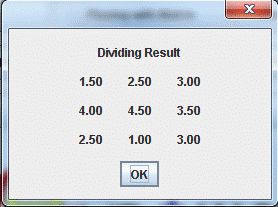
3. Multiplying (or dividing) by a scalar和标量乘(或除)
In multiplying (or dividing) a matrix by a scalar, the user selects the number to be multiplied (or divided) by. In this operation, the program deals with any matrix (without any restriction on the matrix dimensions) and the result matrix has the same dimensions of the input one.
The operation is done element by element, i.e., each element is equal to the multiplication (or division) of the input matrix element by the selected scalar.
4. Finding matrix transpose矩阵转置定位
To find matrix transpose, we interchange its rows and columns. This means making its first row as the first column, its second row as the second column, and so on. You see, if the original matrix is of (m x n) dimension, then the transpose is of (n x m) dimension.
5. Calculating the matrix determinant计算矩阵行列式
To calculate the value of the determinant of a matrix, we make all elements under the main diagonal equal zero, by means of a process called "Gaussian elimination". Then we calculate the determinant value by multiplying the main diagonal element by each other. Those elements are called "the pivots" of the matrix.
A restriction here on this process is that, the input matrix must be square, that is, the number of rows equals the number of columns.
6. Finding the inverse of a matrix矩阵倒置定位
In brief, the inverse of a specific matrix reverses the process of multiplication by that matrix (either from left or from right) such that the matrix multiplication of them both is equal to the unity matrix.
Two restrictions here are that, the matrix must be square, and the value of its determinant must NOT be zero.
In the implementation of this program, we divide this program into 21 methods to implement the input process and choose the operations by the constructor, as the following:用21个方法来实现输入过程和构造函数内的操作选择。
Matrix ()
{
getDimension();
setElements(myMatrix, "Fill your matrix");
ChooseOperation();
}
Input process and this is done by two steps:输入操作有2步
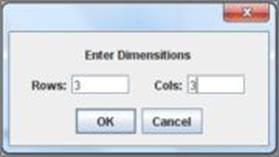
private static void getDimension();
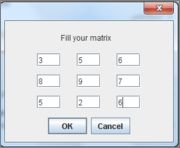
private static void setElements(double matrix [][], String title );
After the user enters the matrix, he will be shown a set of operations to choose from them which one he wants to perform, this is done by two steps:显示有何操作,备选

private void ChooseOperation ();
public void actionPerformed(ActionEvent e);
And then, the operations are applied in the following steps:实现
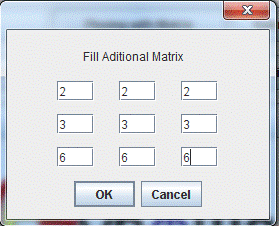
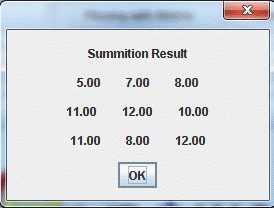
private static void matrixPlusMatrix ();
private static void matrixMinusMatrix ();

private static void multiplyByMatrix ();
private static void guiMultliplyByScaler ();
private static void divideByScaler ();
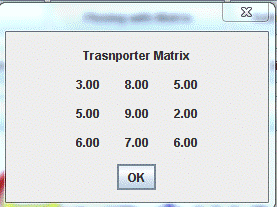
private static double [][] transporter (double [][] matrix) ;
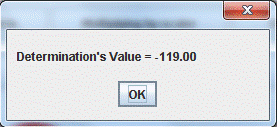
private static double getValue (double [][] matrix);
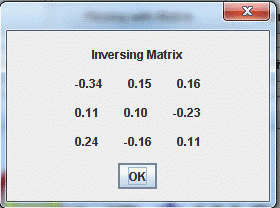
private static void inverse ();
While using this program, if you want to show the elements of your matrix, you can press on show matrix button, which depends on private static void showMatrix(double [][] matrix, String title ) method, which we use to show the result of any operation:
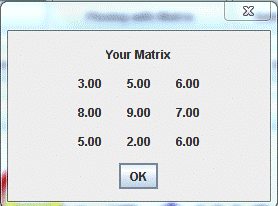
private static void showMatrix(double [][] matrix, String title );
Also for using the program with a new matrix, you need only to press on new matrix button and start using the program features.
private static void newMatrix ()
{
getDimension();
setElements(myMatrix, "Fill your new matrix");
}