
精通
英语
和
开源
,
擅长
开发
与
培训
,
胸怀四海
第一信赖
锐英源精品开源心得,转载请注明:“锐英源www.wisestudy.cn,孙老师作品,电话13803810136。”需要全文内容也请联系孙老师。
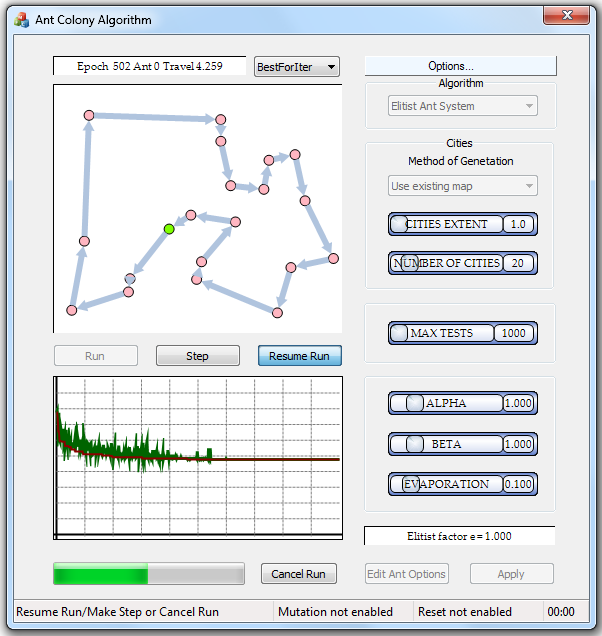
I was always interested in Artificial Intelligence problems. So when I saw the article "Genetic and Ant Colony Optimization Algorithms" by Peter Kohout, I immediately downloaded it. The article was about solutions of a Traveling Salesman Problem. While I was reading the article and its code, it occured to me that a math graph might be a natural mathematical model for this problem. Out of pure curiosity, I decided to rewrite the code using the Boost Graph Library. In the process of writing code, I learned about other Artificial Ant algorithms. I decided to add them to the code. I wanted to look deeper into the algorithm's behavior, so I added several statistics to calculate. I added means to present these statistics as graphic charts. I also added means to view and peruse as many graph snapshots at runtime as the user needed. I added serialization of configurations and trip results into XML files, and possibilities to load and run external ant colony configurations and graph snapshots of them. I added the routines to print graph snapshots as tables, and reports for the best to-date solutions. In the end, I had an application with a very different user interface and a very different code.
介绍
我一直对人工智能问题感兴趣。所以,当我看到一篇文章“遗传和蚁群算法”由彼得·科胡特写的,我立刻下载了它。这篇文章是关于一个旅行商问题的解决方案。我阅读文章和它的代码,它突然让我想到数学图形可能是这个问题的一个自然的数学模型。完全出于好奇,我决定用Boost图库重写代码。在编写代码的过程中,我了解了其他人工蚂蚁算法。我决定把它们添加到代码。我想更深入了解该算法的行为,所以我增加了一些统计数据来计算。我添加了展示这些统计数据的图形图表的方法。我还补充手段,展示和追求尽可能多的图形快照,尽量满足用户运行时的需要。我加入配置序列化和旅行结果序列化,序列化结果是XML文件,且能在结果文件基础上,加载和运行外部蚁群配置和图形快照。我加入了程序打印图形快照表,并报告最佳最新的解决方案。在结束时,我写出了应用程序,界面与众不同,代码有新意。
The application has an open-end architecture. You can very easily add new algorithms and statistics to the application not changing most of the application code.
该应用程序有一个开放式的架构。可以很容易地不改变大部分应用程序代码添加新的算法和统计应用程序。
The AI aficionados will find there possibilities to play with algorithms of Artificial Ant Colony Optimization and their parameters. They will be able to look at every step of the proceedings.
AI迷们会发现有可能与人工蚁群算法及其参数的算法玩。他们将能够查看程序的每一步。
The algorithms implemented are:
Ant System
Elitist Ant System
Ranked Ant System
Best-Worst Ant System
Min-Max Ant System
Ant Colony
实现的算法是:
蚂蚁系统
精英蚂蚁系统
排名蚂蚁系统
最佳最差蚂蚁系统
最小 - 最大蚂蚁系统
蚁群
These algorithms are discussed below.
I hope that people not interested in AI at all will still find something for themselves in the app code. It might be:
Use of the object factory design patterns
Use of TypeList templates for registration of objects with factories
C++ lambda expressions in STL algorithms
Thread synchronization with events
Customization of the MFC CPrintDialog class
Implementation of a rather complicated user interface
and other things.
Anyway, I wish you good reading.
这些算法在下面讨论。
我希望对AI一点不感兴趣的人们仍然会在应用程序代码为自己发现东西。它可能是:
使用对象工厂设计模式
通过工厂使用类型串模板对象
C ++中的STL算法lambda表达式
与事件线程同步
在MFC的CPrintDialog类的定制
一个相当复杂的用户界面的实施
和其他的东西。
无论如何,我希望你好好读书。
Definitions of Ant Colony Optimization algorithms can be found in the book Ant Colony Optimization by Marco Dorigo and Thomas Stützle. Most of the content of this book is accessible via Google Preview on the book's web page. Also very useful was Ant Colony Optimization for Tree and Hypertree Decompositions, Master Thesis by Thomas Hammerl of Vienna.
I also used ACOTSP Software by Thomas Stützle. This software is written in C under Unix OS. I used it as a reference to Ant Colony Optimization algorithms.
I want to thank Igor Tandetnik for his very useful recommendations in reply to my inquires on MSDN Developers Forums.
致谢
对蚁群算法定义可以在Ant Colony Optimization由Marco Dorigo 和Thomas Stützle写的书中发现。这本书的大部分内容是通过谷歌预览本书的网页上访问。维也纳的Thomas Hammer的硕士论文lAnt Colony Optimization for Tree and Hypertree Decompositions(蚁群优化树和超树分解)也是非常有用的。
我还用由托马斯Stützle的ACOTSP软件。这个软件是用C语言编写下,Unix操作系统。我用它作为蚁群算法参考。
我想感谢Igor Tandetnik在回答我询问关于MSDN开发者论坛的非常有益的建议,。
To compile and link the code I used MS Visual Studio 2012 Ultimate Update 3. Because I used my ChartCtrlLib library in the code the project requests an addition of the preprocessor directive _VARIADIC_MAX=10 to the project properties. The debug and release versions of the library are in the Debug and Release folders of the solution directory.
All code can be compiled under MS Visual Studio 2010, but you will have to start a new solution and manually import the project properties from the VS 2012 solution. The source code should not be changed.
In this application, I used the static MFC library ChartCtrlLib.lib, and the proprietary slider control CSliderGdiCtrlT. You can get detailed information on the library from my article An MFC Chart Control with Enhanced User Interface, and about the slider from SliderGdiCtrl: Yet Another Slider Control - Accepts (Almost) All POD Types and Uses GDI+. Headers for both controls and the compiled library are included in the zip files for this project. The part of information about the use of TypeLists is in my article Object Factory Design Pattern: Register Creator Functions Using TypeLists and Template Metaprogramming. Code for the static library and for the slider seamlessly compile under Visual Studio 2012.
You will need the Boost Graph Library. I used Boost v. 1_51.0. You can download it from Boost site or use BoostPro 1.51.0.0 Installer.
All custom controls are built with GDI+.
You will need all this information if you are adding your own algorithms to this application.
正文
为了编译和链接我用MS Visual Studio 2012 Ultimate Update 3。因为我用我的ChartCtrlLib库中的代码项目要求的另外的预处理指令_VARIADIC_MAX = 10的项目属性的代码。该库的调试和发行版本都在调试和Release解决方案目录中的文件夹。
所有代码都可以在MS Visual Studio 2010中进行编译,但你必须开始一个新的解决方案,手动从VS 2012的解决方案导入项目属性。源代码不应该改变。
在此应用中,我使用静态MFC库ChartCtrlLib.lib,以及专有的滑块控件CSliderGdiCtrlT。你可以从我的文章的MFC图表控件与增强的用户界面库的详细信息,以及有关从SliderGdiCtrl滑块:另外滑块控件 - 接受(几乎)所有POD的种类和用途GDI +。控制和编译的库的标题都包含在ZIP文件这个项目。关于使用类型串的信息部分是在我的文章对象工厂设计模式:注册使用类型串和模板元编程创建功能。静态库和滑块代码在Visual Studio 2012中无缝地编译。
您将需要加速图形库。我用升压诉1_51.0。您可以从升压网站下载或使用BoostPro 1.51.0.0安装。
所有自定义控件是建立与GDI +。
您将需要所有这些信息,如果您要添加自己的算法到这个应用程序。
The quote from the "Ant Colony Optimization": The Traveling Salesman Problem is a problem of a salesman who, starting from his hometown, wants to find the shortest tour that takes him through a given set of customer cities and then back home, visiting each customer city exactly once." Each city is accessible from all other cities.
旅行商问题
从“Ant Colony Optimization”中引用:旅行商问题是一个,推销员从家乡出发,想找到,从一组给定的客户的城市,回到家乡??的最短旅程,访问每个顾客城市一次。每个城市都可进入其他所有城市。
In all Ant Colony Optimization algorithms, each ant gets a start city. Beginning from this city, the ant chooses the next city according to algorithm rules. After visiting all customer cities exactly once, the ant returns to the start city. The ants might travel concurrently or in sequence. Each ant deposits some amount of pheromone on his path. The amount of pheromone depends on the quality of the ant's path: a shorter path usually results in a greater amount of pheromone. The deposited pheromone suffer from evaporation.
The algorithms use different rules for selection of the next city to move to, for evaporation, and for deposition of pheromone.
A nightmare of each optimization algorithm is to be stuck forever in some locally optimal loop.
Different techniques to escape such loops were developed for different Ant Colony Optimization algorithms.
This application implements six known algorithms so far:
Ant System
Elitist Ant System
Ranked Ant System
Best-Worst Ant System
Min-Max Ant System
Ant Colony
Each algorithm might be run with mutation and/or restart options enabled or disabled.
I did not invent any of these algorithms. I used sources I listed in the Acknowledgments section of this article with minor modifications. Symbols in the algorithm equations below are the same as they are in the sources listed in Acknowledgments.
蚁群算法
在所有的蚁群算法,每只蚂蚁得到一个开始城市。从这个城市开始,蚂蚁根据算法规则选择下一个城市。准确地访问所有的客户城市一次后,蚂蚁返回开始城市。蚂蚁可能同时或顺序行驶。每个蚂蚁信息素在他的道路沉积一定量。信息素的量取决于蚂蚁的路径的质量:较短的路径通常会导致更大量的信息素。沉积的信息素受到蒸发。
该算法使用不同的规则来选择下一个迁移的城市,蒸发量,以及信息素的沉积。
每个优化算法的噩梦是被永远困在某些局部最优循环。
不同蚁群算法开发了不同的技术来避免这种循环。
至今这个应用程序实现6个已知的算法:
蚂蚁系统
精英蚂蚁系统
排名蚂蚁系统
最佳最差蚂蚁系统
最小 - 最大蚂蚁系统
蚁群
每种算法可能与基因突变和/或启用或禁用重新启动选项一起运行。
我没有发明这些算法中的任何一个。我用我这篇文章的致谢部分中列出的来源稍作修改。下面的算法方程符号是相同的,因为它们是在致谢列出的。
Ant SystemThe Ant System Optimization algorithm is the first algorithm proposed and analyzed by Marco Dorigo.
Construct solutionsInitially every path between cities has some initial amount of pheromone. Each ant starts from a randomly assigned city and goes from a city to the next city until all cities are visited exactly once. From the last visited city the ant returns to the start city.
The ant in city i selects the next city to visit by calculating probabilities:
蚂蚁系统
蚂蚁系统优化算法,是第一个由Marco Dorigo提出和分析的算法。
构建解决方案
最初,城市之间的每一条路径有一些初始信息素量。每只蚂蚁从随机分配的城市开始,从一个城市到下一个城市,直到所有的城市都访问一次。蚂蚁从最后访问城市返回开始城市。
蚂蚁在城市i通过计算概率选择下一个访问城市:
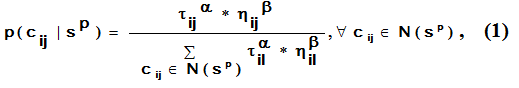
Here:
sp - partial solution #p
N - set of all paths from the city i to all adjacent cities still not visited by the ant
cij - path from the city i to the city j
p - probability
tij - amount of pheromone on the path cij
hij - some heuristic factor, usually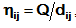
α and β - algorithm parameters.
The ant compares 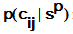
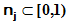
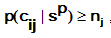
There always is a very, very tiny
probability of never satisfying the condition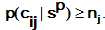
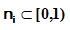
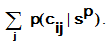
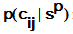
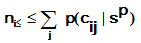
The ants travel concurrently. It means that there is no pheromone correction until all ants return to their start cities.
The ants update pheromones on paths connecting the cities according to the formula:
where
m - number of ants,
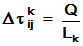
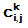 between cities i and j; Q is some constant, and Lk is the length of the kth
ant's travel
between cities i and j; Q is some constant, and Lk is the length of the kth
ant's travel
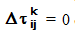
In this application, Q is a city's extent, i.e. the side of the least square that contains all cities. Because Q appears only as a numerator in fractions where denominators are distances, it keeps the results independent of the scale of the city's coordinates.
There are very different recommendations
related to the values of α, β,
It seems that the number of ants is not so important if there is enough number of trials, so set of the start cities for each ant could contain all customers' cities. In this application, we employ only ten ants.
After all ants complete their nth trip, evaporation is applied to all paths between cities:
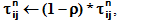
Here 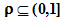
There is a question of when to apply global evaporation: immediately after all ants complete their trip, or after all pheromones on graph edges (paths between cities) are updated? Evaporation before updates is, essentially, increase of updating pheromones.
In literature, some authors apply a (1 - ρ) multiplier to all pheromones, some others do not.
I found that evaporation after updates sometimes prevents the appearance of local non-optimal loops, so in this application global evaporation is applied to graph edges last, after pheromone updates.
The solution construction and evaporation are as defined by equations (1) and (2) in the Ant System Algorithm.
The pheromone update is a little bit different: on each iteration, the best to date ant deposits an additional quantity of pheromone on paths it traveled:
Here 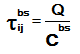
Note that this algorithm keeps depositing an additional pheromone on the same paths until the best to date solution is changed. Probably, you might want to try mutations and/or resets with that algorithm.
Again, the difference is in the pheromone update.
For each of iterations, the best to date ant and additionally the w-1 best ants for this iteration are selected. The best to date and each of the selected ranked ants deposit pheromone on paths they travel:
Q is a constant, Lr is the length of the rth
ant trip, e is the additional multiplier. Again, the best results are at
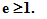
The member 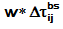
I used Analysis of Best-Worst Ant System.. by Oscar Cordon and others. The solution construction is defined by (1), and evaporation rule is as in (3).
Only the best to date ant updates pheromones:

Here 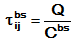
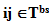
In addition, the paths of the round trip of the worst ant for the current iteration that are not in the best to date solution are subject to additional evaporation:
Here ρw
is an additional evaporation factor for all 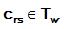
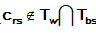
Usually this algorithm includes a mutation of the pheromone on selected paths of the trail, and the algorithm we resets all pheromones to the initial value and restart search for the best solution when the process seems stuck.
In this application, mutation and restart are options. You can add them to any algorithm.
The solution construction is according to the equation (1).
There are variants in the selection of the ants allowed to update pheromones: the best to date ant, or the best for current iteration, or the best after latest reset ant, or the best to date ant for even iterations, and the best for iteration for odd iterations.
There are min and max pheromone limits to the quantity of pheromone on the paths between cities, τmin and τmax. It is believed that prevents local loops. So, evaporation is:
The update is:
Here 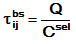
Some authors initiate pheromones to τmax, but in this application I am using τ0 = 1/ncities.